This simplistic example will explain how to use the combination of Custom Constraints, Indicator Constraints, and Linear Ranges.

When we run optimization, we tell the optimizer to try multiple options of configuring the supply chain, calculate statistics for each of them, and find the best solution, or configuration, in terms of profit. The profit in this case is called the Objective Function.

Optimizations that we run always have some constraints, which means the pool of solutions we look for is restricted by factors like demand, number of sites, possible flow throughputs, storage limits, etc. Most of these constraints are available in anyLogistix out-of-the-box. To reflect the special traits of your network you can define your own Custom Constraints.

The user-defined restrictions are created with the help of the following tables: Custom Constraints, Indicator Constraints, and Linear Ranges.

In this simplistic example, we want to set the minimum storage amount a site should have (100 items) if there is a flow through it.

For this, we can use Indicator Constraints, which are if-then statements that define the required condition. The conditions in our case are two possible SC configurations. The optimizer will compare the best solutions from each configuration and choose the best one. Let’s see how they work.

So we need to include the two following cases in the Indicator Constraints table:

1. The flow exists. We want the optimizer to mandatory set the storage to 100 items for all solutions with existing flow through this site.
2. The flow does not exist. In this case there’s no requirement for the storage; the optimizer simply will not suggest to store anything, because storing reduces profit. The only real requirement is the zero value of the actual flow, which will eliminate the necessity of any inventory level. In other words, we must make sure that the flow does not exist.

To define the If and Then components we will use the Custom Constraints and Linear Ranges tables.

First, let’s turn to the Custom Constraints table.

The Custom Constraints table allows us to define conditions that limit the solutions we’re looking for during optimization. These conditions are defined in the form of inequalities.

In the left part of the inequality you can:

• Declare variables.
• Set expressions with standard variables or user-defined variables that users can define in different places.

In the right part of the inequality you can:

• Set an expression or define a function, the value of which will be compared to the left-hand side.

Since we define a binary condition (the flow either exists or not), we will have to set a binary (boolean) variable in the Custom Constraints table. Let’s give it a meaningful name. Name it FlowExists. A boolean variable defines if a flow exists or not by taking the values of 1 (true) and 0 (false) respectively.

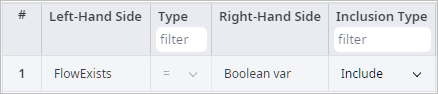
We have set FlowExists as a boolean variable, and now we need to define its values in the Linear Ranges table. This will allow us to reference specific situations when FlowExists equals 1 or 0.

The Linear Ranges table defines which values can be taken by which variables in the form of ranges. We will set this up in the following way:

• If the range for FlowExists is from 1 to 1, it can only become 1 (name this range R: FlowExists=1).
• If the range for FlowExists is from 0 to 0, it can only become 0 (name this range R: FlowExists=0).

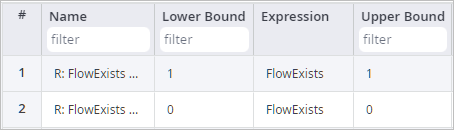
We have finally defined the If statements, now we define the Then statements. We will again use the Linear Ranges table for this.

Let’s start with naming the variables that the Then statements will be referencing (the storage and the flow).

Any storage or flow can be assigned a name in the Product Flows and Product Storages tables. This is used for referencing them in other tables.

We will name the flow and the storage Supplying_DC and DC_Stock respectively.

The Product Flows table:

The Product Storages table:

Now we go back to the Linear Ranges table to define two linear ranges referencing the newly created variables:

1. If the product flow exists, the storage should contain 100 items. Name the new range R: Storage = 100. Set the lower and upper bounds to 100, which means that the storage should always have 100 items. Then define the expression by setting the Variable to DC_Stock and leaving its default coefficient set to 1.
2. For the 0 product flow, create a linear range R: Flow = 0. We are using the Supplying_DC variable in the expression. The upper and lower bounds should be set to 0, limiting the storage amount to 0.

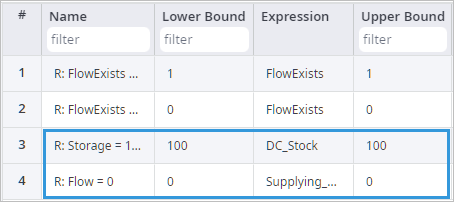
There, the ranges are defined. Now, we need to go to the Indicator Constraints table and connect Ifs and Thens, referencing the Linear Ranges we have just created.

Set the conditional expressions in the Indicator Constraints table

• Case one. IF (R: FlowExists=1) THEN (R: Storage = 100).
• Case two. IF (R: FlowExists=0) THEN (R: Flow = 0).

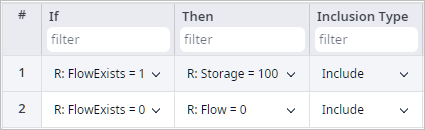
So what happens when we run the optimization?

Each line in the Indicator Constraints table stands for a subset of solutions the optimizer checks. In our case it will sequentially try to find the best solution for the case when we have a product flow through the Dublin DC (and we are obliged to carry a storage), and when there is no flow through this site. In the latter case it doesn't matter if the site carries a storage or not, but the optimizer will likely exclude the variants with the storage since they're more costly, and the primary goal is profit.

Run the optimization and observe the results. As you can see, there is a product flow through Dublin DC. The site’s storage contains 100 items. The optimizer suggested this solution, because it is impossible to fulfil the demand without the flow through this site.

We can check if our constraints really worked by adding another DC with no storage requirement. If we add an alternative site that has no storage limitation, and run the optimization experiment again, we will see that the optimizer chose the 2^nd DC for supplying the customers. This means that there was no flow through the original DC and no storage on any of the sites. The custom constraint worked as expected.

In this way, we can model many special rules in a supply chain using the flexibility of custom constraints, indicator constraints, and linear Ranges.

How can we improve this article?

Send